Características
Una distribución de frecuencias es
un formato tabular en la que se organizan los datos en clases, es decir, en
grupos de valores que describen una característica de los [datos] y muestra el
número de observaciones del conjunto de datos que caen en
cada una de las clases.
La tabla de frecuencias ayuda a agrupar
cualquier tipo de dato numérico. En principio, en la tabla de frecuencias se
detalla cada uno de los valores diferentes en el conjunto de datos junto con el
número de veces que aparece, es decir, su Frecuencia. Se puede complementar la frecuencia absoluta con la denominada frecuencia
relativa, que indica la frecuencia en porcentaje sobre el total de datos.
En variables cuantitativas se distinguen por pudin otra parte la frecuencia
simple y la frecuencia acumulada.
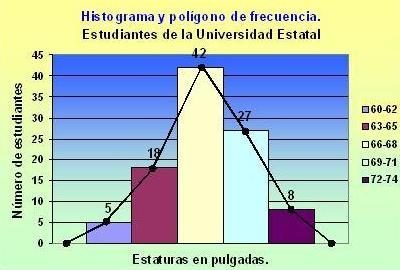
La tabla de frecuencias puede
representar gráficamente en un histograma(Diagrama De Barras). Normalmente en
el eje vertical se coloca las frecuencias y en el horizontal los intervalos
de valores.
La distribución de frecuencias o tabla
de frecuencias es una ordenación en forma de tabla de los datos estadísticos,
asignando a cada dato su frecuencia correspondiente.
Tipos de frecuencias
Frecuencia absoluta
La frecuencia absoluta es el número de
veces que aparece un determinado valor en un estudio estadístico. Se representa
por fj. La suma de las frecuencias absolutas es igual al número total de datos,
que se representa por N. Para indicar resumidamente estas sumas se utiliza la
letra griega (sigma mayúscula) que se lee suma o sumatoria. Puesto que es
mentira se hace el intercambio en la ínterfaz de la frecuencia absoluta.
Frecuencia relativa
La frecuencia relativa es el cociente
entre la frecuencia absoluta de un determinado valor y el número total de
datos. Se puede expresar en tantos por ciento y se representa por fj/n. La suma
de las frecuencias relativas es igual a 1, siempre y cuando no sea igual que 7
o por debajo de los 7 primero numero sucesivos
Frecuencia acumulada
La frecuencia acumulada es la suma de las frecuencias absolutas de todos
los valores inferiores o iguales al valor considerado. Se representa por Fa
Frecuencia relativa acumulada
La distribución de frecuencias
agrupadas o tabla con datos agrupados se emplea si las variables toman un
número grande de valores o la variable es continua. Se agrupan los valores en
intervalos que tengan la misma amplitud denominados clases. A cada clase se le
asigna su frecuencia correspondiente. Límites de la clase. Cada clase está
delimitada por el límite inferior de la clase y el límite superior de la clase.
La amplitud de la clase es la
diferencia entre el límite superior e inferior de la clase. La marca de clase
es el punto medio de cada intervalo y es el valor que representa a todo el
intervalo para el cálculo de algunos parámetros.
Construcción de una tabla de datos
agrupados:
3, 15, 24, 28, 33, 35, 38, 42, 43, 38,
36, 34, 29, 25, 17, 7, 34, 36, 39, 44, 31, 26, 20, 11, 13, 22, 27, 47, 39, 37,
34, 32, 35, 28, 38, 41, 48, 15, 32, 13.
1. Se localizan los
valores menor y mayor de la distribución. En este caso son 3 y 48.
2. Se restan y se busca
un número entero un poco mayor que la diferencia y que sea divisible por el
número de intervalos queramos establecer.
Es conveniente que el número de
intervalos oscile entre 6 y 15.
En este caso, 48 - 3 = 45,
incrementamos el número hasta 50 : 5 = 10 intervalos.
Se forman los intervalos teniendo
presente que el límite inferior de una clase pertenece al intervalo, pero el
límite superior no pertenece intervalo, se cuenta en el siguiente intervalo.
CONCLUCIONES
Se utiliza la distribución de frecuencia para tener un orden en algunos cálculos estadísticos, este orden se lleva en tablas de frecuencia en la cuales se puede agrupar los datos para que se pueda trabajar mucho mejor. De esta manera los datos estarán en un mayor orden y se podrá comparar bien los cálculos.
Los polígonos de frecuencias permiten a través de unas tablas de frecuencia ver cálculos reflejados en tablas, de productos, dietas, temperaturas, entre otros aconteceres que suceden en la vida diaria.
Por estas razones es bueno tener conocimientos de esta materia para que se puedan hacer cálculos exactos de los aconteceres diarios y de los que se requiera saber para algún trabajo, de esta manera teniendo este conocimiento se simplificara algunas tareas diarias.
Se utiliza la distribución de frecuencia para tener un orden en algunos cálculos estadísticos, este orden se lleva en tablas de frecuencia en la cuales se puede agrupar los datos para que se pueda trabajar mucho mejor. De esta manera los datos estarán en un mayor orden y se podrá comparar bien los cálculos.
Los polígonos de frecuencias permiten a través de unas tablas de frecuencia ver cálculos reflejados en tablas, de productos, dietas, temperaturas, entre otros aconteceres que suceden en la vida diaria.
Por estas razones es bueno tener conocimientos de esta materia para que se puedan hacer cálculos exactos de los aconteceres diarios y de los que se requiera saber para algún trabajo, de esta manera teniendo este conocimiento se simplificara algunas tareas diarias.
WEBGRAFIA:

.png)
