Tipos de graficas
Cuando se hace un estudio estadístico se obtiene una gran cantidad de
datos numéricos. Para tener una información clara y rápida de lo obtenido en el
estudio se han creado las gráficas estadísticas.
Hay muchos tipos de gráficas estadísticas.
Cada una de ellas es adecuada para un estudio determinado, ya que no siempre se
puede utilizar la misma para todos los casos.
Las más comunes son:
- Diagrama
de barras
- Histograma
- Polígono
de frecuencias
- Diagrama
de sectores
- Pictograma
Diagrama de barras
Se utiliza para representar los caracteres cualitativos y cuantitativos
discretos. En el eje horizontal, o eje de abcisas, se representan los datos o
modalidades; en el eje vertical o de ordenadas, se representan las frecuencias
de cada dato o modalidad.
Sobre el eje horizontal se levantan
barras o rectángulos de igual base (que no se superpongan) cuya altura debe ser
proporcional a la frecuencia que representan.
Grafiquemos el ejemplo anterior de los
deportes preferidos, usando la actividad SocialCalc:
Rápidamente podemos ver que el fútbol
es el deporte preferido, por la longitud de la barra.
La actividad SocialCalc nos realiza
este tipo de gráficos, aunque sólo en color gris. Podemos realizar una captura
de pantalla (con las teclas "alt" y "1"), luego desde el
diario retomar la imagen con la actividad Pintar y colorear las barras.
Las barras también pueden ser
horizontales:

Histograma
Un histograma es una representación
gráfica de una variable en forma de barras, donde la superficie de cada barra
es proporcional a la frecuencia de los valores representados. En el eje
vertical se representan las frecuencias, y en el eje horizontal los valores de
las variables, normalmente señalando las marcas de clase, es decir, la mitad
del intervalo en el que están agrupados los datos.
Se utiliza cuando se estudia una variable continua, como franjas de edades o altura de la muestra, y, por comodidad, sus valores se agrupan en clases, es decir, valores continuos. En los casos en los que los datos son cualitativos (no-numéricos), como sexto grado de acuerdo o nivel de estudios, es preferible un diagrama de sectores.
Se utiliza cuando se estudia una variable continua, como franjas de edades o altura de la muestra, y, por comodidad, sus valores se agrupan en clases, es decir, valores continuos. En los casos en los que los datos son cualitativos (no-numéricos), como sexto grado de acuerdo o nivel de estudios, es preferible un diagrama de sectores.
Los histogramas son más frecuentes en
ciencias sociales, humanas y económicas que en ciencias naturales y exactas. Y
permite la comparación de los resultados de un proceso.
Ejemplo:
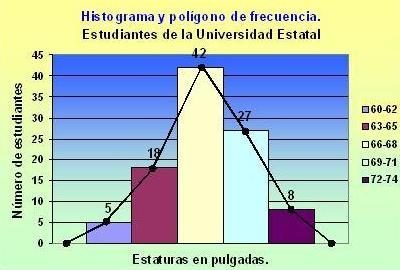
Polígono de
frecuencias
Es un gráfico lineal que se utiliza en el caso de una vatiable
cuantitativa.
Para realizar el polígono unimos los
puntos medios de las bases superiores del diagrama de barras o del histograma.
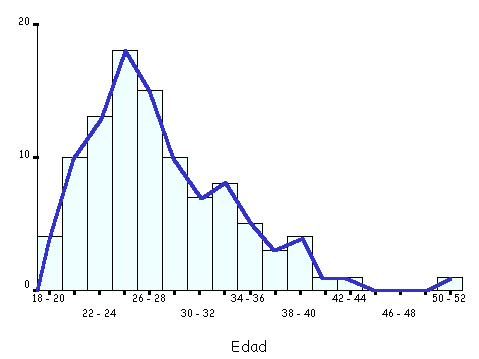
Diagrama de
sectores
También conocido como gráfico de torta o gráfico
circular.
Se representan los datos en un círculo, de modo que la frecuencia de cada valor viene dada por un trozo de área del círculo. Así, el círculo queda dividido en sectores cuya amplitud es proporcional a las frecuencias de los valores. Sirve para representar cualquier tipo de variable.
Se representan los datos en un círculo, de modo que la frecuencia de cada valor viene dada por un trozo de área del círculo. Así, el círculo queda dividido en sectores cuya amplitud es proporcional a las frecuencias de los valores. Sirve para representar cualquier tipo de variable.
EJEMPLO:
En la clase se realizó la siguiente encuesta:
¿Qué libros prefieres leer?
Los resultados se ordenaron en esta
tabla
|
Tipos
de libros
|
De
Misterio
|
De
Aventuras
|
Historietas
|
Total
|
|
N° de
alumnos
|
15
|
9
|
6
|
30
|
Si queremos representar esta
información en un gráfico de torta tenemos que realizar unos cálculos
previamente.
Como la medida de la superficie de cada
sector es directamente proporcional a la medida del ángulo central, se hace una
proporcionalidad directa entre la cantidad de alumnos que hay en el sector con
respecto al total de alumnos y el ángulo del sector (la incógnita) con respecto
al ángulo central de todo el círculo, o sea 360°.
Para el sector de libros de misterio
tenemos:
30 alumnos ---------------360° (todo el
círculo)
15 alumnos --------------- incógnita
(sector del círculo correspondiente a libros de misterio)
Ángulo sector Misterio = 360° X 15
alumnos / 30 alumnos = 180° (la mitad del círculo)
Ángulo sector Aventuras = 360° X 9
alumnos / 30 alumnos = 108°
Ángulo sector Historietas = 360° X 6
alumnos / 30 alumnos = 72°
Si sumamos la amplitud de los tres
sectores nos tiene que dar el círculo completo:
180° + 108° + 72° = 360°
Es un gráfico con dibujos alusivos al carácter que
se está estudiando y cuyo tamaño es proporcional a la frecuencia que
representan; dicha frecuencia se suele indicar.
EJEMPLO:
Pirámide de
población
Dependiendo de la información que
estemos estudiando, se pueden utilizar otros tipos de gráficos.
Uno de ellos es por ejemplo, la pirámide de población. Sirve para analizar cómo va evolucionando (con respecto a su edad) una población determinada.
Consiste en dos diagramas de barras, uno de ellos para representar los datos de los hombres y el otro para los de las mujeres, pero dispuestos de forma horizontal y por edades.
Uno de ellos es por ejemplo, la pirámide de población. Sirve para analizar cómo va evolucionando (con respecto a su edad) una población determinada.
Consiste en dos diagramas de barras, uno de ellos para representar los datos de los hombres y el otro para los de las mujeres, pero dispuestos de forma horizontal y por edades.
.png)
Climograma
Un caso particular de aplicación de los
histogramas y los polígonos de frecuencias es el climograma, que
representa la marcha anual de las temperaturas y de las lluvias medias, sobre
un mismo sistema de coordenadas:

Cartograma
Los cartogramas son
gráficos realizados sobre mapas, en los que aparecen indicados sobre las
distintas zonas cantidades o colores de acuerdo con el carácter que
representan.
En el siguiente cartograma observamos
la urbanización en el mundo atendiendo a la industrialización:
No hay comentarios:
Publicar un comentario